平行
\(\)2直線が交わってできる4つの角のうち,向かい合った角を
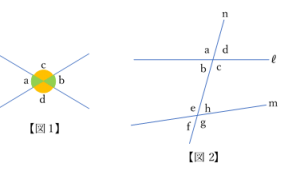
対頂角という。図1において,\(\angle a\:\)と\(\angle b\:\),\(\angle c\:\)と\(\:\angle d\:\)はそれぞれ対頂角である。対頂角の大きさは,それぞれ等しい。
2直線ℓ, mにもう一つの直線 n が交わって図2のように 8つの角ができたとき,\(\angle a\)と\(\angle e\)のような位置関係にある角を同位角という。図2において,\(\angle b\)と\(\angle f\),\(\angle c\)と\(\angle g\),\(\angle d\)と\(\angle h\)もそれぞれ同位角である。\(\angle b\)と\(\angle h\)のような位置関係(2つの直線の内側)にある角を錯角という。\(\angle c\)と\(\angle e\)も錯角である。
平行線と錯角・同位角の関係
二つの直線 ℓ, m に,一つの直線 n が交わるとき,
- 二つの直線 ℓ,m が平行なら,同位角は等しく,錯角も等しい。
- 同位角が等しいなら,二つの直線ℓ,mは平行である。
- 錯角が等しいなら,二つの直線ℓ,mは平行である。

図3において,ℓ//m なら,a = b(同位角), a = c(錯角)
逆に同位角が等しい(a = b)なら,ℓ // m
錯角が等しい(a = c)なら,ℓ // m
例題
下の図において,\(\angle x\), \(\angle y\) の角度をそれぞれ求めなさい。ただし,2直線ℓとmは平行(ℓ//m)とする。


解答

同位角は等しいので,\(\angle a\:=\:45°\)
対頂角は等しいので,\(\angle b\:=\:75°\)
\(\begin{eqnarray} \angle a + \angle b + \angle x &=& 180° \\ 45 + 75 + \angle x&=& 180 \\ \angle x &=& 180 – 120 \\ &=& 60 \end{eqnarray} \)
\(\begin{eqnarray} \angle y + \angle b &=& 180 \\ \angle y &=& 180 – 75 \\ &=& 105 \end{eqnarray} \)

この種の問題では,元々の平行線と平行に補助線を引く(直線 n)。
上図で,\(\angle a + \angle b \:=\: \angle x \)
\(\angle c\)と\(\angle a\),\(\angle d\)と\(\angle b\)はそれぞれ平行線の錯角であり,それぞれの角の組は等しい。また,対頂角の関係から,
\(\angle c = 30°.\:\angle d = 45°\)であるので,\(\angle a\:=\:30°,\:\angle b\:=\:45°\)
したがって,\(\angle x = 30 + 45 = 75°\)
\(\angle y + 30 = 180\) より,\(\angle y = 150°\)
図形と角度(内角・外角)
三角形
下図の\(\triangle ABC\)において,辺BCを延長した直線上に点Dをとる。このとき,\(\angle CAB\), \(\angle ABC\), \(\angle BCA\)を\(\triangle ABC\)の内角,\(\angle ACD\)を頂点Cにおける外角という。

三角形の外角は,となりにない三角形の二つの内角の和に等しい。
(上図では,外角c = 内角a + 内角b, 外角b = 内角c + 内角a, 外角a = 内角b + 内角c)
三角形の内角の和は,180°である。(内角a + 内角b + 内角c = 180°)
隣り合う内角と外角の和は180°である。(内角c + 外角c = 180° など)
すべての外角の和は 360°である。(外角a + 外角b + 外角c = 360° )
三角形で,すべての内角が鋭角なものを 鋭角三角形,一つの角が直角であるものを 直角三角形,一つの角が鈍角であるものを 鈍角三角形 という。

多角形
多角形(4角以上)は,一つの頂点から引いた対角線によって,複数の三角形に分けられる。より具体的には,四角形の場合は,一つの頂点から一本の対角線を引き,二つの三角形に分けられる。五角形の場合は,一つの頂点から二本の対角線を引き,三つの三角形に分けられる。n角形は,一つの頂点から引いた対角線によって,(n-2)個の三角形に分けられる。したがって,n角形の内角の和は 180×(n-2) 度である。

[ n角形のある頂点と,その頂点の両隣を除いて,他の (n – 3)個の頂点に向けて,n-3 本の対角線を引くと,n角形は,n – 2 個の三角形に分割できる。実はこれには,細かい条件があり,星型の多角形等,凹みがある多角形では,対角線の引き方にコツがあるのですが,ここでは,すべての多角形は突多角形であると考えて下さい。]
また,n角形のすべての外角の和は 360度である。
⇒ となり合う内角と外角の和は180度で,すべての内角と外角の組を足して,内角の和を引くと,180×n – 180×(n-2) = 360 度
例題
解答
- 二つの考え方を示します。(根本的には同じことを言ってます。)

【考え方1】「三角形の外角の大きさは,外角の隣にない2つの内角の和に等しい」という関係を利用する。
三角形の内角と外角の関係から,
\(\begin{eqnarray} \angle CAB + \angle ABC &=& \angle ACD \\ x + 70 &=& 120 \\ x &=& 120 – 70 \\ &=& 50 \end{eqnarray} \)
【考え方2】「三角形の内角の和は,\(180°\)である」ことを利用する。\(3点B, C, D は一直線上にあるので,\)
\(\begin{eqnarray} \angle BCA + \angle ACD &=& 180 \\ \angle BCA &=& 180 – 120 \\ &=& 60 \end{eqnarray} \)
三角形の内角の和は 180 度であるので,
\(\begin{eqnarray} \angle CAB + \angle ABC + \angle BCA &=& 180 \\ x + 70 + 60 &=& 180 \\ x &=& 180 – (70+60) \\ &=& 50 (°)\end{eqnarray} \)
- 二つの三角形に着目して,不明な角を徐々に明らかにします。

線分BCとDEの交点をFとする。
\(\triangle CAB において,\)
\(\angle BCA = 180 – \angle DCB = 180 – 80 = 100 (°)\)
\(\angle CAB = 30 (°)\)
であるので,\(\angle ABC = 50 (°)\)
\(次に,\triangle FEB において\)
\(\angle BFE = 180 – 100 = 80 (°)\)
三角形の内角の和は180°であるので,
\(\begin{eqnarray} x + \angle EBF + \angle BFE &=& 180 \\ x + 50 + 80 &=& 180 \\ x &=& 80 (°)\end{eqnarray} \)
- いわゆるブーメラン型の角度の求め方です。

2点ADを結び,その延長上に点Eをおきます。
このとき,\(\angle BDE (\angle a) は,\triangle DAB において,頂点Dにおける外角であり,\)
\(\angle CDE (\angle b) は,\triangle DCA において,頂点Dにおける外角である。\)
それぞれの三角形において,内角と外角の関係より,
\(\begin{eqnarray} \angle a &=& \angle DAB + \angle ABD … ① \\ \angle b &=& \angle CAD + \angle DCA … ② \end{eqnarray} \)
\(① + ② より,\)
\(\begin{eqnarray} \angle a + \angle b &=& \angle DAB + \angle CAD + \angle ABD + \angle DCA \\
\angle x &=& \angle CAB + \angle ABD + \angle DCA \\ &=& 55 + 25 + 35 \\ &=& 115 (°) \end{eqnarray} \)
-
四角形ABCDにおいて,内角の和は 360° であるので,
\(\begin{eqnarray} \angle A + \angle B + \angle C + \angle D &=& 360 \\ 2a + 100 + 110 + 2b &=& 360 \\ 2a + 2b &=& 150 \\ a + b &=& 75 \;\dots\;①\end{eqnarray} \)
三角形AEDにおいて,内角の和は 180° であるので,
\(\begin{eqnarray} \angle EAD + \angle ADE + \angle DEA &=& 180 \\ a + b + x &=& 180 \\①より,75 + x &=& 180 \\ x &=& 105 \end{eqnarray} \)
合同な図形
合同な図形
二つの図形が合同とは,それらの形と大きさが同じであることです。合同な図形を構成するパーツ(辺,弧,角等),それぞれ対応付けることができ,図形の移動(平行移動,回転移動,胸像移動)を行うと,ぴったり重ねることができます。
言い換えると,
- 対応する線分の長さは等しい。
- 対応する角の大きさは等しい。
- 合同な円は,半径が等しい。

上図の三つの四角形は合同です。四角形ABCD を少し右回転(時計回り)すると四角形EFGH 重なり,
四角形EFGH を裏表ひっくり返して回転すると,四角形IJKL に重なります。
それぞれの図形が合同であるとき 記号「≡」を使って次のように表記します。
四角形ABCD ≡ 四角形EFGH
四角形EFGH ≡ 四角形IJKL
また,図形を表す際に使用する頂点は,右辺と左辺でそれぞれ対応する頂点の順に表記します。
正しく表記することにより,どの辺(どの角)が対応して合同になっているかも読み取れます。
三角形の合同条件
図形の証明
命題「A ならば, B である」といった記述で,A の部分を仮定,B の部分を結論といい,
仮定で与えられた条件と,正しいことが認められている事項(根拠)を利用して,結論を導くことを証明という。
図形の証明の際に,根拠として利用できる事項は,今までに学習した事項になりますが,証明でよく利用される事項は次のようになります。
図形の基本的性質
図形の証明をする際に,利用される明らかな事項(根拠)となります。
-
- 対頂角は等しい
- 平行線に関わる性質
⇒ 平行線の同位角,錯角は等しい
⇒ 同位角, 錯角が等しいなら平行
- 三角形の性質
⇒ 内角,外角の関係
⇒ 正三角形の角度,辺の長さ
⇒ 二等辺三角形の性質(底角が等しい等)
- 三角形の合同条件
- 平行四辺形の性質
- ひし形の性質
また,数量,数式に関わる次のような式も,既知(あたりまえ)の事項として証明なしに利用することができます。
- \(・a=b,\:b=c\:ならば\:b\:=\:c\)
\(・a\:=\:b\:ならば\:a+c\:=\:b+c\)
\(・a+c\:=\:b+c\:ならば\:a\:=\:b\) 等々
その他,今後,図形や数式に関わる定理や性質を,いくつも習うことになりますが,基本的にこれらの事項は証明をする際に事実として証明なしに利用することができます。逆に,証明をするためには,定理や性質は覚えておく必要があります。
例題
図のように,2つの直線\(\:ℓ,\:m\:\)が交わっており,\(ℓ,\:m\:\)の交点を\(A\), 点 A から同じ距離の \(ℓ,\:m\:\)上に点 B, C があり,\(\angle BAC\)の二等分線を\(n\)とし,\(n\)上に点 D をとる。このとき,\(BD\:=\:CD\:\)であることを証明しなさい。

解答
[解説]
・この証明問題の仮定は,次の2つである。
- 点B, Cはそれぞれ2直線\(\:ℓ,\:m\:\)上に,点Aから等距離にある。
⇒ \(AB\:=\:AC\)
- 直線\(\:n\:\)は,\(\angle BAC\)の二等分線である。
⇒ \(\angle BAD\:=\:\angle CAD\)
・この証明問題の結論は,\(BD\:=\:CD\:\)である。
※ 線分の長さが等しいことを示すために,よく利用されているのは,該当する線分をそれぞれ辺とする2つの図形が合同であることを示すことです。(「合同な図形の対応する辺の長さは等しい」ことを利用する。)
[証明]
(2点C, D および 2点B, Dをそれぞれ結んで,二つの三角形\(\triangle ABD\:と\:\triangle ACD\)に着目する。)

\(\triangle ABD\:と\triangle ACD\:\)において,
仮定より,
\(\begin{eqnarray} \angle BAD &=& \angle CAD \;\dots\;① \\ AB &=& AC \;\dots\;② \\共通な辺なので,AD &=& AD \;\dots\;③ \end{eqnarray} \)
①,②,③より,2組の辺とその間の角が,それぞれ等しい ので,
\(\triangle ABD\:≡\:\triangle ACD\)
合同な図形の対応する辺の長さは等しいので,
\(BD\:=\:CD\)










 https://oyaji3.net/study/studymath/chu2math/examine_figures/
https://oyaji3.net/study/studymath/chu2math/examine_figures/
 oyaji3.net
oyaji3.net








