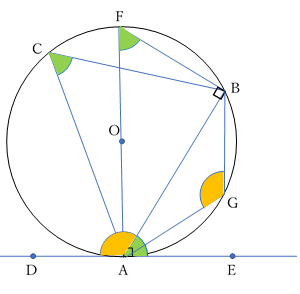
円周角・中心角・弦
\(\)
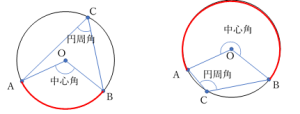
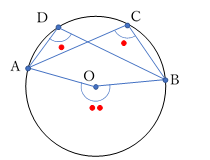
円 O の円周上の異なる 3点 A, B, C に対して，点C から点A および 点B に線分を引く。
また，中心 O から，点A および 点B に線分を引く。
このとき，
\(\angle ACB\:を\:\stackrel{\Large \frown}{AB}\:\) に対する円周角，
\(\angle AOB\:を\:\stackrel{\Large \frown}{AB}\:\) に対する中心角，
線分ABを弦という。
なお，上図のように，\(\stackrel{\Large \frown}{AB}\) は，円周上の長い方，短い方のいずれでも，または，3点A, O, B が直線上(直径上)にあっても，本ページで示す定理等は成り立ちます。
円周角の定理
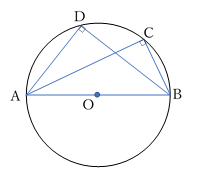
- 1つの弧に対する円周角の大きさは，その弧に対する中心角の大きさの半分である。
- 同じ弧に対する円周角の大きさは等しい。
- この定理はABが直径上(AOBが一直線)にあるときも成り立ち，このとき，∠AOBは180°で，その時の円周角は 90° である。
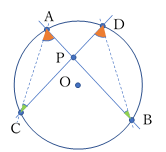
円周角の定理の逆
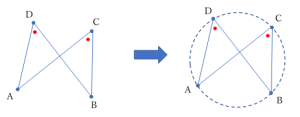
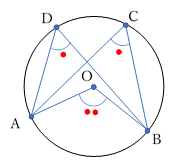
図のような配置で，異なる 4点 A, B, C, D があり，
\(\;\;\angle ACB\:=\:\angle ADB\) のとき，4点 A, B, C, D は同一円周上にある。
\(\;\;\angle ACB\:=\:\angle ADB\) のとき，4点 A, B, C, D は同一円周上にある。
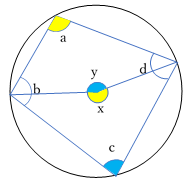
円に内接する四角形
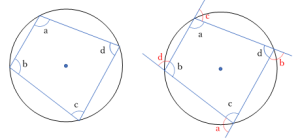
- 円に内接する四角形の対角の和は 180° である。
→ a + c = 180°, b + d = 180° - 円に内接する四角形の外角は，対角(内角)に等しい。
→ a の外角は c の角度と同じ。
証明
ここでは，a + c = 180 を説明(証明)します。
\(円周角：\angle a\: に対応する中心角は\:\angle x\)
\(円周角：\angle c\: に対応する中心角は\:\angle y\)
であるので，
\(a\:=\:\frac{x}{2},\:c\:=\:\frac{y}{2}\:\)。
この2式を足すと，\(a\:+\:c\:=\:\frac{x + y}{2}\) であるが，
\(x + y\:=\:360°\:\)であるので，\(a + c\:=\:180°\)
\(円周角：\angle a\: に対応する中心角は\:\angle x\)
\(円周角：\angle c\: に対応する中心角は\:\angle y\)
であるので，
\(a\:=\:\frac{x}{2},\:c\:=\:\frac{y}{2}\:\)。
この2式を足すと，\(a\:+\:c\:=\:\frac{x + y}{2}\) であるが，
\(x + y\:=\:360°\:\)であるので，\(a + c\:=\:180°\)
円と直線
円と接線
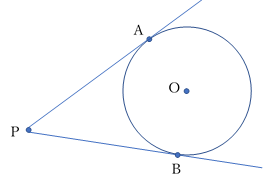
図のように，円の外側の 1点P から円の接線を2本引いた時，点P と 接点A, B の長さは等しい。( AP = BP )
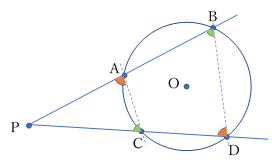
方べきの定理
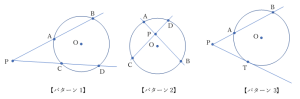
図のように，円周上の点 A, B, C, D, T がある。
【パターン１】と【パターン２】は，点Pを通る2本の割線(円との交点が2点ある線)を引いたもの。
【パターン３】は，点Pが円の外部にあり，Pを通る接線とPを通る割線を引いたもの。
このとき，PA, PB, PC, PD, PT の長さには，次の関係が成り立ちます。
\(PA\times PB\:=\:PC\times PD, または，PA\times PB\:=\:PT^2\)
証明
【方針】
【パターン１】と【パターン２】は，\(\triangle PAC\) ∽ \(\triangle PDB\)，【パターン３】は，\(\triangle PAT\) ∽ \(\triangle PTB\) を示して，それぞれ，辺の長さの比から上記の等式を示します。
【証明】
【パターン１】
\(\triangle PAC\:\)と\(\triangle PDB\:\)において，円に内接する四角形の外角の大きさは，その頂点に対する対角の大きさに等しい(「円に内接する四角形の角度」参照)ので，
\(\;\;\angle PAC\:=\:\angle PDB\)
\(\;\;\angle PCA\:=\:\angle PBD\)
2組の角がそれぞれ等しいので，\(\triangle PAC\:\)∽\(\triangle PDB\)
よって，\(PA\::\:PC\:=\:PD\::\:PB\) となり，
\(PA\times PB\:=\:PC\times PD\)
【パターン２】
\(\triangle PAC\)と\(\triangle PDB\:\)において，同じ弧に対する円周角は等しいので，
\(\;\;\angle PAC\:=\:\angle PDB\)
\(\;\;\angle PCA\:=\:\angle PBD\)
2組の角がそれぞれ等しいので，\(\triangle PAC\:\)∽\(\triangle PDB\)
よって，\(PA\::\:PC\:=\:PD\::\:PB\) となり，
\(PA\times PB\:=\:PC\times PD\)
【パターン3】
\(\triangle PAT\)と\(\triangle PTB\)において，接弦定理より，\(\angle PTA\:=\:\angle PBT\)
共通の角であるので，\(\angle TPA\:=\:\angle BPT\)
2組の角がそれぞれ等しいので，\(\triangle PAT\:\)∽\(\triangle PTB\)
よって，\(PA\::\:PT\:=\:PT\::\:PB\) となり，
\(PA\times PB\:=\:PT^2\)
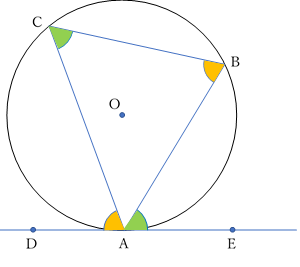
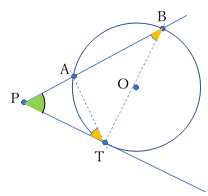
接線と弦のなす角は，その弦に対する円周角に等しい。
図で説明すると，
\(\angle BAE\:=\angle ACB\)
\(\angle CAD\:=\:\angle ABC\)
証明
[方針] 接線と弦の角度が鋭角の場合，直角の場合，鈍角の場合に分けて証明します。
[接線と弦のなす角度が鋭角の場合] 図の緑色の角の場合です。
図のようにAFが直径となるように点Fをとると，線分AFは円の直径であるので，
\(\angle ABF\:=\:90°\) [直径の円周角は直角] 三角形の内角の和は 180°であるので，
\(\angle FAB + \angle AFB + \angle ABF \:=\: 180°\) より，
\(\angle FAB\:=\:90°-\angle AFB\)… ①
また，直線DEは円の接線であるので，
\(\angle EAF\:=\:90°\)
\(\angle FAB\:=\:\angle EAF – \angle BAE\:=\: 90° – \angle BAE\)… ②
①，②より，\(\angle AFB\:=\:\angle BAE\)
円周角の定理より，\(\angle AFB\:=\:\angle ACB\)
したがって，\(\angle ACB\:=\:\angle BAE\)
\(\angle ABF\:=\:90°\) [直径の円周角は直角] 三角形の内角の和は 180°であるので，
\(\angle FAB + \angle AFB + \angle ABF \:=\: 180°\) より，
\(\angle FAB\:=\:90°-\angle AFB\)… ①
また，直線DEは円の接線であるので，
\(\angle EAF\:=\:90°\)
\(\angle FAB\:=\:\angle EAF – \angle BAE\:=\: 90° – \angle BAE\)… ②
①，②より，\(\angle AFB\:=\:\angle BAE\)
円周角の定理より，\(\angle AFB\:=\:\angle ACB\)
したがって，\(\angle ACB\:=\:\angle BAE\)
[接線と弦のなす角度が直角の場合]
直径を弦とする弧の円周角になり，この場合は円周角は直角になる。
[接線と弦のなす角度が鈍角の場合] 図の黄色の角の場合
\(\angle BGA\)は，四角形AGBCの点Cに対角になるので，
\(\angle BGA\:=\:180° – \angle BCA\) … ③
接線と弦のなす角度が鋭角の場合に証明済みの，
\(\angle BCA\:=\:\angle BAE\) であるので，
③は次のようになる。
\(\angle BGA\:=\:180° – \angle BAE\) … ④
また, \(\angle DAB + \angle BAE = 180°\) より，
\(\angle DAB\:=\:180° – \angle BAE\) … ⑤
④，⑤より，\(\angle BGA = \angle DAB\)