因数分解
→ たとえば,63 は,3 × 21 で,21 は 3 × 7 です。3 と 7 はともに素数なので,他の数を使った素数の積にはできません。結局 63 を素因数分解すると,3 × 3 × 7 = \(3^2 × 7 \) となります。
次に,式の因数分解を考えます。 文字式(多項式)において,各項に共通な因数があるとき,その式は共通因数でくくることができます。これは,式の展開とは逆の操作をすることで,多項式を掛け算の形に変形する操作です。これを式の因数分解といいます。
→ たとえば,ax + ay は,共通因数:a でくくることができ,ax + ay = a(x + y) となります。これは,式の展開の項で示した操作とは逆になります。(結合法則) また,\( a^2b + 2ab + ab^2 = ab(a + b + 2) \) は,共通因数: ab でくくっています。
式を因数分解するには,式の展開の項で示した,乗法公式 (の逆)を利用します。式の展開は,分配法則にしたがった操作を行えば何とかなりましたが,因数分解するには結合法則だけではなかなか結論までたどり着きません。乗法公式の利用が必要です。 以下に,乗法公式の右辺と左辺を入れ替えたものを示します。因数分解は,左辺から右辺の形を作ることです。乗法公式で示した通り,1 と 2,および,3 と 4 は 本質的には同じで,式は3パターンになります。
- \(x^2 + (a + b)x + ab = (x + a)(x + b)\)
- \(acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)\)
- \(a^2 + 2ab + b^2 = (a + b)^2\)
- \(a^2\: – \:2ab + b^2 = (a\: – \:b)^2\)
- \(a^2\: – \:b^2 = (a + b)(a\: – \:b)\)
以下に,因数分解の基本手順を示します。例題がないと,何のことかわからないかもしれませんが,あとの説明をみると理解できると思います。
- 共通因数でくくる
- 乗法公式を利用できないか
- 置換してみて,乗法公式を利用できないか
- たすき掛けしてみる
- 解の公式を利用する [ 2次方程式の項で習います ]
次の式を因数分解しなさい。
(1) \(3ax^2\: – \:6axy + 3ay^2\)
(2) \(a^2b + ab\: – \:12b\)
(3) \(a^2\: – \:b^2 + c^2\: – \:d^2 + 2ac\: – \:2bd\)
(4) \(5x^2 + 18x + 16\)
(1)について。 最初の問題にしては長い式と思われるかもしれませんが,公式や手順を使えば,わりと簡単にとけます。
各項の数値部分は 3 または 6 なので,すべて,3 の倍数です。また,各項には a が含まれているので,共通因数は「3a」です。
手順1 「共通因数でくくる」 を行うと,元の式は次のように変形できます。
\(3ax^2\: – \:6axy + 3ay^2 = 3a ( x^2\: – \:2xy + y^2) \)
元の式は,掛け算の形に変形できました。でも,因数分解は,ここで完了ではありません。
手順2 乗法定理をあてはめることを考えます。
\((x^2\: – \:2xy + y^2)\)
は,公式:4 の a, b を a = x, b = y で置き換えたものと同じ式になります。そこで,公式:4 を利用してかっこ内の式を因数分解します。
\((x^2\: – \:2xy + y^2) = (x\: – \:y)^2\)
したがって,元の式は次のようになります。
\(3ax^2\: – \:6axy + 3ay^2 = 3a ( x\: – \:y )^2 … (答)\)
※ これ以上 結合法則(乗法公式の逆)を適用できないところまで,因数分解しないと正解となりません。
次に (2) の問題です。
共通因数が b であるので,まずは,次の式に変形します。
\(a^2b + ab\: – \:12b = (a^2 + a\: – \:12)b \; … \; (1)\)
右辺のかっこ内を,公式:1 にあてはめることを考えます。公式:1が主張していることは,式の形が
\(x^2 + ○ x + △ \)
の形の式は,和が ○ , 積が △ になる数値をみつけると,因数分解できるよ。。。ということです。
問題の式 (1) のかっこ内は,\(a^2 + a\: – \:12\) であり,和が1,積が -12 になる数を求めれば良いのです。
積が -12 になる2つの数の組み合わせは,
(1, -12), (2, -6), (3, -4), (4, -3), (6, -2), (12, -1)
の 6 通りですが,このうち,足して 1 になるのは,(4, -3) のみです。
したがって,和が1, 積が -12 になる数の組は,4 と -3 です。これを公式: 1 にあてはめると,
\(a^2 + a\: – \:12 = (a + 4)(a\: – \:3)\)
となります。これを (1) 式に代入して,
\(a^2b + ab\: – \:12b = (a + 4)(a\: – \:3)b \; … \; (答)\)
となります。
[ 注意 ] この問題の解答途中で,積が -12 になるものとして,6組の整数の対を示しました。でも,乗法公式は,各文字が整数という条件は限定していません。各文字が整数に限らず,分数や小数であっても,さらには,後で習う無理数であっても,乗法公式は成り立ちます。因数が上記のやり方で求まれば,解答として成り立ちますが,上記のやり方で因数が求まらない場合,因数分解できないとは限りません。次に(3)です。
全ての項に対する共通因数はないので,公式にあてはめることを考えます。全ての項を一気にまとめられる公式もなさそうなので,各項を並べかえたり,部分的に分けることを考えます。
次のように与えられた式を2つの部分に分けます。(+で結合した項と – で結合した項 にまとめて,順序を入れ替えます。)
\(a^2\: – \:b^2 + c^2\: – \:d^2 + 2ac\: – \:2bd = (a^2 + 2ac + c^2)\: – \:(b^2 + 2bd + d^2)\)
右辺の二つのかっこ内は,ともに,公式:3 を適用できることがわかり,次のように式変形できます。
\((a + c)^2\: – \:(b + d)^2\)
ここで,x = a + c, y = b + d とおくと,上記の式は次のように変形でき,これは,公式:5を使って下の行の右辺のようになります。
\((a + c)^2\: – \:(b + d)^2 = x^2\: – \:y^2 = (x + y)(x\: – \:y)\)
この最右辺の x, y に,x = a + c, y = b + d を代入すると
\((x + y)(x – y) = ((a + c) + (b + d))((a + c)\: – \:(b + d)) = (a + c + b + d)(a + c\: – \:b\: – \:d) = (a + b + c + d)(a\: – \:b + c\: – \:d)\)
となり,元の式は \((a + b + c + d)(a\: – \:b + c\: – \:d)\) に因数分解できました。
この問題の解答では,途中,x = a + c, y = b + d とおいて,式をわかり易く変形しました。ここが,本問題のポイントです。慣れてきたら,簡単な置き換えは頭の中でやれるようになるかもしれないけど,できれば,置き換えをしたことを答案に記載し,残しておいた方がよいかと思います。
(4) についてです。 \(5x^2 + 18x + 16\)
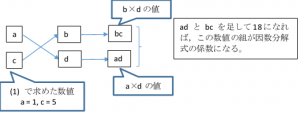
公式:2に当てはめれば良いのですが,ac = 5, ad + bc = 18, bd = 16 を満たす a, b, c, d を求めるのはどうすれば良いのかということになります。ここでは,2つの解法を示します。
[解法1] たすきがけ
(考え方) \(5x^2 + 18x + 16 を (ax + b)(cx + d)\) の形にしたい。
右辺を展開すると,\( acx^2 + (ad + bc)x + bd\) となり,これが,問題で与えられた式と等しくならなければならないので,ac = 5, bd = 16 となる数値の組のうち,ad + bc = 18 となるものが見つかれば,見つかった a, b, c, d の値を 上記の右辺 に代入すればよい。
(1) 2次\((x^2)\)の係数から,a, c の候補を求める
2次(\( x^2 \)の係数は 5 で,5 は素数なので,掛けて 5 になるのは,1 × 5 か (-1)×(-5) (逆順も含む)だけである。
したがって,a = 1, c = 5 または a = 5, c = 1 であるが,前者の場合だけを考えて,以下の手順を行えばよい。負数の場合も,ここでは考える必要はない。
(2) 定数項から b, d の候補を求める
定数項は 16 であり,掛けて 16 になる整数の組は,(1, 16), (2, 8), (4, 4), (-1, -16), (-2, -8), (-4, -4) である。a, c を正の数にしているので,下記の手順(3)から,負の数の組み合わせにならないことは,想像つきますね。(もし,b, d が負の数の組なら,ad も bc も負になるので,ad + bc も負になり,ad + bc = 18 とはならない。)
(3) たすき掛け計算(ad + bc)をして,元の係数に合致するものを求める
上記の (1) で求めた数値の組を縦に並べ,その右側に,(2) で求めた数値の組を,順次,縦に並べて たすき掛け 計算し,それぞれの数値の和を求めます。( ad + bc の値を求め,これが 18 になるものを探す。) 条件を満たす数値の組は,ひとつだけ求めれば手順終了です。
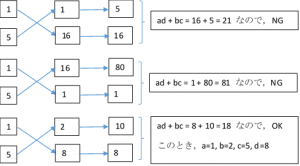
ここまでの操作で,因数分解したときの 各項の係数(a, b, c, d)が求まりました。この値を (ax + b)(cx + d) に代入して,次の結論が導き出せます。
\(5x^2 + 18x + 16 = (x + 2)(5x + 8) … [答] \)
[注意] この方法も,各項の係数が整数であることを前提に計算をしています。a, b, c, d が整数であることは,どこでも保証されていないので,上記の方法では,答が導き出せないこともあることに留意して下さい。
[方法2] 二次方程式の「解の公式」の利用
(考え方) 二次方程式: \(ax^2 + bx + c = 0\)の二つの解を p, q とすると,この方程式の左辺は次のように表すことができます。
\(ax^2 + bx + c = a(x\: – \:p)(x\: – \:q)\)
(p または q を代入したとき,上記の式の値は 0 になることを示しています。)
この式は,元の方程式の解が判れば,因数分解可能であることを意味しています。
解の公式を使うと方程式: \(ax^2 + bx + c = 0\) の解は次の通りです。
\(x = \frac{-b\pm\sqrt{b^2\: – \:4ac}}{2a} \)
\(5x^2 + 18x + 16 = 0\) の解は,上記の解の公式の a, b, c にそれぞれ,a = 5, b = 18, c = 16 を代入して,次のようになります。
\(x = \frac{-18\pm\sqrt{18^2\: – \:4×5×16}}{2×5} \)
\(\;\;\: = \frac{-18\pm2}{10} = \:-2, \:-\frac{8}{5} \)
したがって,元の式は,次のように変形(因数分解)できます。
\(5x^2 + 18x + 16 = 5(x\: – \:(-2))(x\: – \:(-\frac{8}{5})) = (x + 2)(5x + 8) \) … [答]
この方法を使えば,計算は大変だけど,各項の係数が整数とはならない場合でも計算は可能になります。ただし,平方根の中が負にならないことを確認する必要があります。(平方根の中が負の場合は,(中学校範囲では) 因数分解不可能) また,平方根の中が平方数である場合は,この方法を使わなくても因数分解は可能となります。
