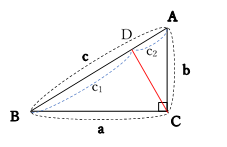
三平方の定理
三平方の定理
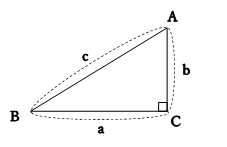
上図のように，直角三角形ABCの直角を挟む2辺の長さを，a, b, 斜辺の長さを c とすると，
辺の長さの間に次の関係式が成り立つ。
\(\;\; c^2\:=\:a^2\:+\:b^2\)
これを，「三平方の定理」または「ピタゴラスの定理」という。
※ 「斜辺」とは，直角に対する辺で，直角三角形で一番長い辺である。
辺の長さの間に次の関係式が成り立つ。
\(\;\; c^2\:=\:a^2\:+\:b^2\)
これを，「三平方の定理」または「ピタゴラスの定理」という。
※ 「斜辺」とは，直角に対する辺で，直角三角形で一番長い辺である。
証明
証明方法は，いろいろありますが，ここでは相似を使った方法を示します。
点\(C\)から辺\(AB\)に下した垂線と,辺\(AC\)との交点を\(D\)とし，\(BD=c_1, AD=c_2\) とする。
\((c = c_1 + c_2)\)
このとき，\(\triangle ABC\) と \(\triangle CBD\) において，共通な角なので，\(\angle ABC\:=\:\angle CBD\)。
また，\(\angle ACB\:=\:\angle CDB\:=\:90°\) であるので，2組の角が等しいので，
\(\;\;△ABC\:\)∽\(\:△CDB\) であり，\(AB\::\:BC\:=\:CB\::\:CD\) より，
\(\;\;c\::\:a\:=\:a\::\:c_1\;→ a^2\:=\:c×c_1 … ①\)
同様に，\(\triangle CAB\) と \(\triangle DAC\) において，共通な角なので，\(\angle CAB\:=\:\angle DAC\),
また，\(\angle ACB\:=\:\angle CDA\:=\:90°\) であるので，2組の角が等しいので，
\(\;\;\triangle CAB\:\)∽\(\:\triangle DAC\)であり，\(CA\::\:AB\:=\:DA\::\:AC\)より，
\(\;\;b\::\:c\:=\:c_2\::\:b\; → b^2\:=\:c×c_2 … ②\)
①，②より，\(a^2\:+\:b^2\:=\:c×c_1+c×c_2\:=\:c(c_1+c_2)\:=\:c^2\)
証明問題で，上記定理の逆 が使われることもありますので，以下に示します。
三平方の定理の逆
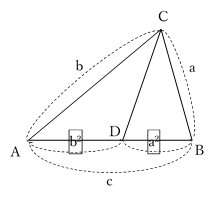
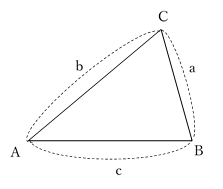
△ABCにおいて，各頂点の対辺の長さを，それぞれ，a, b, c とする。このとき，
\(\;\; a^2 + b^2 = c^2\:\)の関係を満たせば，△ABC は，∠C = 90° の直角三角形である。
(図は，わざと，∠C が直角でないように描いています。)
\(\;\; a^2 + b^2 = c^2\:\)の関係を満たせば，△ABC は，∠C = 90° の直角三角形である。
(図は，わざと，∠C が直角でないように描いています。)
証明
いろんな証明がありますが，ここでは，相似を利用します。
辺ABを \(b^2\::\:a^2\) に内分する点を D とする。
(ここでは，作図可能かどうかは問題にしません。図中に，四角で囲んで\(\:a^2\:\)や\(\:b^2\:\)が書いてありますが，これは，線分の長さを意味しておらず，線分の長さの比を意味しています。)
(ここでは，作図可能かどうかは問題にしません。図中に，四角で囲んで\(\:a^2\:\)や\(\:b^2\:\)が書いてありますが，これは，線分の長さを意味しておらず，線分の長さの比を意味しています。)
すると，
\(\;\;AD\:=\:c\times\frac{b^2}{a^2+b^2} (ACの長さに対して，\frac{b^2}{a^2 + b^2} の比率)\:=\:c\times\frac{b^2}{c^2}\:=\:\frac{b^2}{c}\)
\(\;\;DB\:=\:c\times\frac{a^2}{a^2+b^2}\:=\:\frac{a^2}{c}\)
となる。
△ABC と △ACD において，
\(\;\;AB\::\:AC\:=\:c\::\:b\)
\(\;\;AC\::\:AD\:=\:b\::\:\frac{b^2}{c}\:=\:c\::\:b\)
であるので，AB：AC ＝ AC：AD が成り立つ。
また，∠BAC = ∠CAD であるから，2組の辺の比と，その間の角が等しいので，
△ABC ∽ △ACD である。
相似な図形の対応する角は等しいので，∠ACB = ∠ADC … ①
同様に，△ABC と △CBD において，
\(\;\;AB\::\:BC\:=\:c\::\:a\)
\(\;\;CB\::\:BD\:=\:a\::\frac{a^2}{c}\:=\:c\::\:a\)
であるから，
AB : BC = CB : BD が成り立つ。
また，∠ABC = ∠CBD であるから，2組の辺の比と，その間の角が等しいので，
△ABC ∽ △CBD である。
相似な図形の対応する角は等しいので，∠ACB = ∠CBD … ②
ここで，∠ADC + ∠CDB = 180° であるので，これと，①，② から，
∠ADC + ∠CDB = 2×∠ACB = 180°
∴ ∠ACB = 90°
直角三角形の辺の比
直角三角形は，鋭角の角度が決まると，三辺の長さの比が同時に決まります。逆に，三辺の長さの比が決まると，鋭角の角度が決まります。下に，代表的な直角三角形(三角定規の2種類の直角三角形)の角度と，辺の長さの比を示します。この辺の長さの比は知っているものとした問題が出題されることもありますので，少なくとも，下記の2種類の直角三角形の角度と，辺の長さの比は覚えましょう。
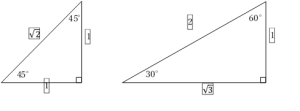
小さい三角形は，底角が45°の二等辺三角形で，辺の長さの比は，\(1:1:\sqrt{2}\)。
大きい三角形は，鋭角が30°と60°で，辺の長さの比は，\(1:\sqrt{3}:2\)。
直方体・立方体の対角線の長さ
三平方の定理 の立体図形への応用として，直方体と立方体の対角線の長さを求める式を以下に示します。
・ 縦，横，高さが，それぞれ，a, b, c の長さの直方体の対角線の長さは，次の式で求まります。
\(\;\;\;\;\;\sqrt{a^2 + b^2 + c^2}\)
・ 1辺の長さが a の立方体の対角線の長さは，次の式で求まります。
\(\;\;\;\;\;\sqrt{3}a\)
・ 縦，横，高さが，それぞれ，a, b, c の長さの直方体の対角線の長さは，次の式で求まります。
\(\;\;\;\;\;\sqrt{a^2 + b^2 + c^2}\)
・ 1辺の長さが a の立方体の対角線の長さは，次の式で求まります。
\(\;\;\;\;\;\sqrt{3}a\)
補足説明
【直方体の対角線の長さ】
上図のように，直方体ABCD-EFGHがあり，AB=a, AD=b, AE=c とすると，面 ABCD の対角線の長さは，\(\sqrt{a^2+b^2}\) である。
また，△ACE は直角三角形であり，三平方の定理から，
\(EC^2 = AC^2 + AE^2 = (\sqrt{a^2+b^2})^2 + c^2 = a^2 + b^2 + c^2\)
\(EC > 0 であるので，EC = \sqrt{a^2 + b^2 + c^2}\)
★★★
立方体については，上記直方体の b = c = a の場合と考えればよいので，
対角線の長さは \(\sqrt{ 3a^2 }\:=\:\sqrt{3}a\) となる。