相似な図形

\(\)

中学3年生の数学で「相似」の単元は，中学で学んだ多くの単元を網羅した問題が作りやすく，幅広い知識や計算技量が必要になる場合があります。

相似な図形

以下の両方の条件を満たす図形を「相似な図形」といいます。図形によっては，全ての条件を満たさなくても，条件の一部を満たせば，自ずと，他の条件が満たされる場合もあります。(後述の三角形の相似条件)

  1. 対応する部分(辺 や 弧)の長さの比はすべて等しい。
  2. 対応する角の大きさは，それぞれ等しい。

※ 言い換えると，形が同じで，拡大・縮小した図形(大きさが違う図形)を「相似な図形」といいます。これに対し，合同な図形は，形も大きさも同じ図形でした。
※ 相似な図形の，対応する部分(辺や半径，弧)の長さの比を「相似比」という。

【相似な図形】円，中心角が同じ扇形，正方形，正五角形，…，球，立方体，…

【相似とは限らない図形】

長方形 … 対応する角の大きさは等しいけど，辺の長さの比が同じとは限らない。

ひし形 … 辺の長さの比は等しいけど，角度が等しいとは限らない。

 

【相似の記号 ∽】
２つの図形が相似であることを表すのに ∽ を使う。これは，英語で相似を意味する「Similar」の頭文字を横にしたものです。日本語でもローマ字に直すと S で始まるので，覚えやすいですね。
△ABC ∽ △DEF，四角形ABCD ∽ 四角形EFGH
[注意点]  ∽ の両辺に記述する頂点は，対応する頂点の順番で記述します。これは合同な図形を記述する際も同じでしたね。

 

三角形の相似条件

ふたつの三角形に対して，次のいずれかの条件が成り立つとき 相似 である。

  • 3組の辺の比がすべて等しい
  • 2組の辺の比と，その間の角がそれぞれ等しい
  • 2組の角がそれぞれ等しい

 

例題 １

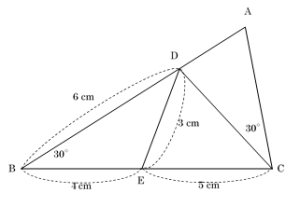
(1) △ABCと相似な三角形はどれですか。

(2) △BEDと相似な三角形はどれですか。

(3) CDの長さを求めなさい。

解答

(1) △ABC と △ACD において，

\(∠ABC\:=\:∠ACD\:=\:30°, 共通な角なので\:∠BAC\:=\:∠CAD\)

2組の角がそれぞれ等しいので，△ABC ∽ △ACD  … (答)

実は，これでは，答としては不十分です。他の三角形，△ABE, △BCD, △CDF, △ACE, △ADE, △BDE が △ABC と相似関係にないことを示していないからです。これらの三角形の中には，見ただけで角度が合わず，明らかに相似ではないものも含まれていますが，…。

他の三角形が，△ABC と相似関係でないことを示すためには，各三角形の内角の角度，または辺の長さ(の比)を調べる必要があります。(3) で 辺CD の長さを求めていますが，線分AD, AC の長さも，△ABC ∽ △ACD の関係から求めることができ，△ABC については，すべての辺の長さを求めることができます。各辺の比と同じ組み合わせにはならないことを示す必要があります。(問題の作り方が悪かったです。)

(2) △BED と △BDC において

BE : BD = 4 : 6 = 2 : 3, BD : BC = 6 : 9 = 2 : 3

したがって，BE : BD = BD : BC

また，∠DBE = ∠CBD であるので，

2組の辺の比とその間の角がそれぞれ等しいので，△BED ∽ △BDC

(3) (2)より，△BED と △BDC の相似比は，2 : 3 であるので，

\(CD\:=\:\frac{3}{2}DE\:=\:\frac{3}{2}×3\:=\:\frac{9}{2} (cm)\)

 

例題 ２

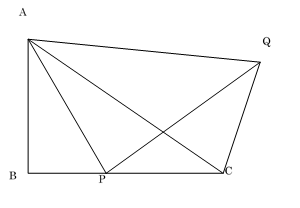
△ABCの辺BC上に点Pがある。△ABC ∽ △APQ であるとき，△ABP ∽ △ACQ となることを証明しなさい。

解答

△ABC ∽ △APQ より，AB : AP = AC : AQ∴ AB × AQ = AP × AC

両辺を AC × AQ でわると，\(\frac{AB}{AC} \:=\: \frac{AP}{AQ}\)

よって，AB : AC = AP : AQ … ①

∠BAC = ∠BAP + ∠PAC … ②

∠PAQ = ∠CAQ + ∠PAC … ③

また，∠BAC = ∠PAQ … ④

②，③，④ より，∠BAP = ∠CAQ … ⑤

②，⑤より，2組の辺の比とその間の角がそれぞれ等しいので，△ABP ∽ △ACQ ■

相似の証明に使う事項
  • 対頂角，平行線における 同位角，錯角
  • 平行線と線分の比
  • 多角形の内角，外角の性質
  • 二等辺三角形の性質
  • 平行四辺形，長方形，ひし形の性質
  • 三角形の相似条件，相似な図形の性質
  • 中点連結定理の利用
  • 面積比

 

平行線と線分の比
【三角形の底辺と平行な線分を引いた時の線分比】

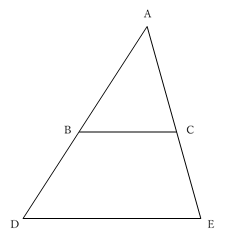
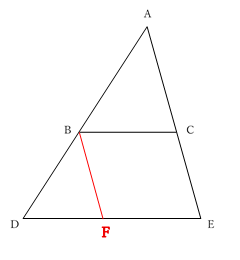
上図において，△ADE の辺 AD, AE 上に，それぞれ点 B, C があるとき，
(1) BC // DE ならば，

\(AB\::\:AD\:=\:AC\::\:AE\:=\:BC\::\:DE\)
\(AB\::\:BD\:=\:AC\::\:CE\)
証明
上の式は，△ABCと△ADEが相似であるので，対応する辺の長さの比が等しいことから証明します。
△ABC と △ADE において，BC // DE であるので，平行線の同位角の関係から，
∠ABC = ∠ADE, ∠ACB = ∠AED であり，
2組の角がそれぞれ等しいので，△ABC ∽ △ADE である。
相似な三角形の対応する辺の長さの比は等しいので，
\(AB\::\:AD\:=\:AC\::\:AE\:=\:BC\::\:DE\)
下の式も基本的には同じですが，ここでは2通りの証明をしてみます。
[証明1] △ABC ∽ △ADE であるので，
\(AB\::\:AD\:=\:AC\::\:AE\)
\(AD\:=\:AB\:+\:BD, \:AE\:=\:AC\:+\:CD であるので\)
\(AB\::\:(AB\:+\:BD)\:=\:AC\::\:(AC\:+\:CD)\)
\(\frac{AB + BD}{AB}\:=\:\frac{AC + CD}{CD}\)
\(1\:+\:\frac{BD}{AB}\:=\:\frac{AC}{CD} + 1\)
\(∴ AB : BD = AC : CD \)
[証明2] 補助線を引いて，もうひとつ，相似な三角形を作ります。
\(点Bを通り，辺CDと平行に線を引き，辺DEとの交点をFとする。\)
\(△ABC と △BDF において，\)
\(BF//CEであるので，∠BFD = ∠CEF (同位角)\)
\(∠ABC = ∠BDF(同位角)\)
\(したがって，2組の角がそれぞれ等しいので，△ABC ∽ △BDF\)
\(∴ AB : BD = AC : BF\)
\(また，BF = CE であるので，AB : BD = AC : CE\)

(2) ★(1)の逆★

\(AB\::\:AD\:=\:AC\::\:AE\;ならば\:BC\://\:DE\)
\(AB\::\:BD\:=\:AC\::\:CE\;ならば\:BC\://\:DE\)

【平行線と交わるふたつの線分が作る線分の比】

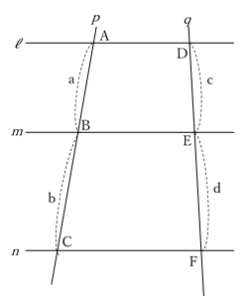
\(ℓ\://\:m\://\:n\: のとき，\)

\(a\::\:b\:=\:c\::\:d\)

\(a\::\:c\:=\:b\::\:d\)

証明のやり方は，点A と 点D が重なるように直線\(\:p\:\)または\(\:q\:\)を平行移動した補助線を引くと，上で示した三角形と同じ形となります。それから，先は上の定理と同様の方法で証明可能です。

 

中点連結定理

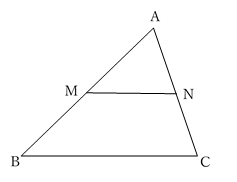
△ABCの2辺AB, ACの中点を，それぞれ，M, N とすると，
MN // BC で， MN = \(\frac{1}{2}\)BC である。

台形についても，似たような定理があります。
(台形の中点連結定理と呼ばれることもあります。)

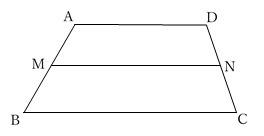
AD // BC の台形ABCD で，2辺AB, CDの中点を，それぞれ，M, N とすると，
MN // BC で，MN = \(\frac{1}{2}\)(AD + BC)

 

相似な図形の面積比と体積比
  • 相似な平面図形の面積比は，相似比の2乗の比に等しい。
  • 相似な立体図形の表面積比は，相似比の2乗の比に等しい。
  • 相似な立体図形の体積比は，相似比の3乗の比に等しい。