y = ax2
\(\)ここでは,二次関数\(\;y \:=\: ax^2\)の性質をまとめます。
\(y\:は\:x\:の2乗に比例するといい,\:x\:の値を\:n\:倍すると,\:y\:の値は \:n^2\: 倍になります。\)
具体的な例をいくつか見ましょう。
【正方形の面積】
1辺が\(\:x\:cm\) の正方形の面積 y \((cm^2)\)は,\(y = x^2\)となり,\(x\:と\:y\:\)の関係を表にすると,次のようになります。\(x\)が2倍,3倍,4倍になると,yは4倍,9倍, 16倍になることが確認できます。
| x (cm) | 1 | 2 | 3 | 4 | 5 | 6 |
| y(\(cm^2)\) | 1 | 4 | 9 | 16 | 25 | 36 |
【扇形の面積】
次に半径\(\:x\:cm\) で中心角が 60° の扇形の面積: y(\(cm^2\))の関係は,\(\:y\:=\:\frac{\pi}{6}x^2\)ですが,これを表にすると,次のようになります。ただし,円周率は 3.14 で計算し,小数点第4位で四捨五入してあります。この場合も,\(x\)が2倍,3倍,4倍になると,yは4倍,9倍, 16倍になることが確認できます。
| x (cm) | 1 | 2 | 3 | 4 | 5 | 6 |
| y(\(cm^2)\) | 0.523 | 2.093 | 4.710 | 8.373 | 13.083 | 18.540 |
【直方体の体積】
1辺が\(\:x\:cm\) の正方形を底面とし,高さが \(2 cm\:\) の立方体の体積 y \((cm^3)\)は,\(y = 2x^2\)となり,\(x\:と\:y\:\)の関係を表にすると,次のようになります。この場合も,\(x\)が2倍,3倍,4倍になると,yは4倍,9倍, 16倍になることが確認できます。
| x (cm) | 1 | 2 | 3 | 4 | 5 | 6 |
| y (\(cm^3\)) | 2 | 8 | 18 | 32 | 50 | 72 |
ここまで,辺の長さと,図形の面積,体積の関係を見てきましたが,次のいずれの式においても,x が正の範囲で値を求めました。
1辺が \(x cm\) の正方形の面積: \(y \:=\: x^2\)
半径が \(x cm\), 中心角60°の扇形の面積: \(y \:=\: \frac{\pi}{6}x^2\)
1辺が \(x cm\) の正方形を底面とする高さ \(2cm\) の直方体の体積: \( y \:=\: 2x^2\)
これらの式の x の範囲を負の値まで拡張して表を作ると,次のようになります。
【\(y \:=\: x^2\)】
| x | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 36 | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
【\(y \:=\: \frac{\pi}{6}x^2\)】
| x | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 18.840 | 13.083 | 8.373 | 4.410 | 2.093 | 0.523 | 0 | 0.523 | 2.093 | 4.710 | 8.373 | 13.083 | 18.840 |
【\(y \:=\: 2x^2\)】
| x | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 72 | 50 | 32 | 18 | 8 | 2 | 0 | 2 | 8 | 18 | 32 | 50 | 72 |
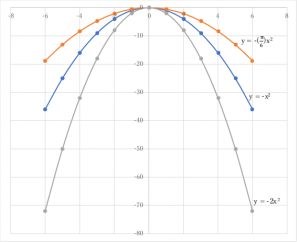
上記,いずれの式も,y の値は x = 0 を中心に左右対称になっていることがわかります。これら3つをグラフに表すと次のようになります。

このようなグラフの形状を「放物線」といいます。グラフからも判るように,\(y \:=\: ax^2\) の a の値が小さければ緩やかなカーブ,a の値が大きければ急なカーブになります。これまでは,\(a > 0\) の場合について見てきましたが,\(a < 0\) の場合は,下のグラフのように,上下が逆の \( y \) の値が 負または 0 の放物線になります。