[旧版] 平成31年 2019 栃木県高校入試数学大問６

この記事は，後半の内容が壊れてしまっていますので，内容を更新して再投稿しました。

新しい投稿はこちらです。

検索などで，このページに来た方には申し訳ありませんが，再投稿版をご参照ください。

ーーーーーーーーーーーーーーーーーー以下旧版

ログ投稿の練習も兼ねて，ワードで編集してみました。

以前，Wordから投稿すると図形が壊れたので，投稿前に図(絵)に変換して投稿してみました。

先頭部分の数字「6」は□で囲み文字にしたのですが，ダメですね。

あとは，ところどころ，改行(改行して欲しくないところで改行)が少し変になってます。

ざっくりと，手動で直してみましたが，まだ，みにくい部分があります。。。

どうも，数式が含まれている投稿は word には不向きかな？？？

６
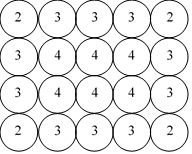
形も大きさも同じ半径1cmの円盤がたくさんある。これらを図1のように，縦m 枚，横n 枚(m, n は3以上の整数)の長方形状に並べる。このとき，4つのにある円盤の中心を結んでできる図形は長方形である。さらに，図2のように，それぞれの円盤は×で示した点で他の円盤と接しており，ある円盤が接している円盤の枚数のその円盤に書く。例えば，図2はm=3, n=4の長方形状に円盤を並べたものであり，円盤Aは2枚の円盤と接しているので，円盤Aに書かれる数は3，円盤Cに書かれる数は4となる。また，m=3, n=4の長方形状に円盤を並べたとき，すべての円盤に他の円盤と接している枚数をそれぞれ書くと，図3のようになる。

このとき，次の1, 2, 3, 4の問いに答えなさい。

m = 4, n = 5のとき，3が書かれた円盤の枚数を求めなさい。

円盤の配置は，図のようになり，3が書かれた円盤の枚数は

全部で10枚である。
m = 5, n = 6のとき，円盤に書かれた数の合計を求めなさい。

円盤の配置は図のようになり，各数字の書かれた枚数と

合計値は，以下の通りになる。

2 が 4枚で合計 8

3 が 14枚で合計 42

4 が 12枚で合計 48

合計の数値は，8+42+48 = 98
m = x, n = x のとき，円盤に書かれた数の合計は440であった。このとき，x についての方程式をつくりx の値を求めなさい。ただし，途中の計算も書くこと。

2が書かれた円盤は4 隅の 4 枚

3が書かれた円盤は周囲の辺上にあり，一辺あたりx – 2 枚なので全部で4( x – 2)枚

4が書かれた円盤は内部の矩形内にあり，全部で(x – 2)²枚

したがって，円盤に書かれた数値の合計を式で表すと次のようになる。

2×4 + 3×{4×(x – 2)} + 4×(x – 2)² = 8 + 12 x – 24 + 4 x ² – 16 x + 16 = 4 x ² – 4 x

これが，440になるので，

4 x ² – 4 x = 440

x ² – x – 110 = 0

(x + 10)(x – 11) = 0

x = -10 または
x = 11

x ≧ 3 より，x = 11
次の文の①，②，③に当てはまる数を求めなさい。ただし，a, bは2以上の整数で，a<bとする。