H31 (2019) 栃木県 高校入試 数学 大問 6 [再投稿]
\(\)本投稿の内容を Word から投稿してみましたが,数式部分が崩れたりしましたので,WordPress のエディタで書き直して投稿します。
6 形も大きさも同じ半径 1cm の円盤がたくさんある。これらを図1のように,縦 \(m\) 枚,横 \(n\) 枚(\(m, n\) は \(3\) 以上の整数)の長方形状に並べる。このとき,4つの角にある円盤の中心を結んでできる図形は長方形である。さらに,図2のように,それぞれの円盤は✖で示した点で他の円盤と接しており,ある円盤が接している円盤の枚数をその円盤に書く。例えば,図2は \(m = 3,\: n = 4\) の長方形状に並べたものであり,円盤Aは2枚の円盤と接しているので,円盤Aに書かれる数は2となる。同様に,円盤Bに書かれる数は3,円盤Cに書かれる数は4となる。また,\(m = 3,\: n = 4\) の長方形状に円盤を並べたとき,すべての円盤に他の円盤と接している枚数をそれぞれ書くと,図3のようになる。
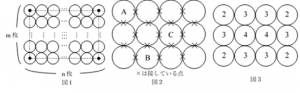
このとき,次の1,2,3,4の問いに答えなさい。
1. \(m\:=\:4,\:n\:=\:5\) のとき,3が書かれた円盤の枚数を求めなさい。
円盤の配置は,下図のようになり,3が書かれた円盤の枚数は全部で 10 枚である。
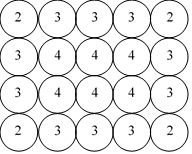
2. \(m = 5,\: n = 6\) のとき,円盤に書かれた数の合計を求めなさい。
円盤の配置は図のようになり,各数字が書かれた枚数と,それぞれの合計値は,以下の通りになる。
2 が 4枚 で 合計 8
3 が 14枚 で 合計 42
4 が 12枚 で 合計 48
円盤に書かれた数値の合計は,8+42+48 = 98
2 が 4枚 で 合計 8
3 が 14枚 で 合計 42
4 が 12枚 で 合計 48
円盤に書かれた数値の合計は,8+42+48 = 98

3. \(m = x,\: n = x\) のとき,円盤に書かれた数の合計は \(440\) であった。このとき,\(x\) についての方程式をつくり \(x\) の値を求めなさい。ただし,途中の計算も書くこと。
2が書かれた円盤は4 隅の 4 枚
3が書かれた円盤は周囲の辺上にあり,一辺あたり\(x\:–\:2\)枚なので全部で\(4(x\:–\:2)\)枚
4が書かれた円盤は内部の矩形内にあり,全部で\((x-2)^2\) 枚
したがって,円盤に書かれた数値の合計を式で表すと次のようになる。
\(\;\;\;\;\;2×4 + 3×{4×(x – 2)} + 4×(x – 2)^2\)
\(\;= 8 + 12 x – 24 + 4 x^2 – 16x + 16\)
\(\;= 4x^2 – 4x\)
これが,\(440\)になるので,
\(4x^2\:–\:4x\:=\:\:440\)
\(x^2\:-\:x\:-\:110\:=\:0\)
\((x+10)(x – 11) = 0\)
\(x = -10 \:または\: x = 11\)
\(x ≧ 3 より,x = 11\)
3が書かれた円盤は周囲の辺上にあり,一辺あたり\(x\:–\:2\)枚なので全部で\(4(x\:–\:2)\)枚
4が書かれた円盤は内部の矩形内にあり,全部で\((x-2)^2\) 枚
したがって,円盤に書かれた数値の合計を式で表すと次のようになる。
\(\;\;\;\;\;2×4 + 3×{4×(x – 2)} + 4×(x – 2)^2\)
\(\;= 8 + 12 x – 24 + 4 x^2 – 16x + 16\)
\(\;= 4x^2 – 4x\)
これが,\(440\)になるので,
\(4x^2\:–\:4x\:=\:\:440\)
\(x^2\:-\:x\:-\:110\:=\:0\)
\((x+10)(x – 11) = 0\)
\(x = -10 \:または\: x = 11\)
\(x ≧ 3 より,x = 11\)
4. 次の文の①,②,③に当てはまる数を求めなさい。ただし,\( a,\: b \) は2以上の整数で,a < b とする。
m = a + 1, n = b + 1 として,円盤を図1のように並べる。4つの角にある円盤の中心を結んでできる長方形の面積が 780 \(cm^2\) となるとき,4が書かれた円盤の枚数は,a = ( ① ), b = ( ② ) のとき最も多くなり,その枚数は ( ③ ) 枚である。
4隅の中心を結んだときの長方形の縦横の長さは,それぞれ,
\(\;\; \begin{eqnarray} (m-1)\times 2 &=& 2a (cm), \\ (n-1)\times 2 &=& 2b (cm) \end{eqnarray} \)
である。
4隅の円盤の中心を結んでできる長方形の面積が \(780 cm^2\) だから,次の式が成り立つ。
\(\;\;\;\; 2a\times 2b\:=\:780\;→\:ab\:=\:195\;\;…[1]\)
4が書かれた円盤は,\(縦\:m\:-\:2\:=\:a\:-\:1\;\)枚,\(横\:n\:-\:2\:=\:b\:-\:1\;\)枚の長方形になるので,全部で,\((a\:-\:1)(b\:-\:1)\)枚である。
\(\;\;\;\; (a\:-\:1)(b\:-\:1)\:=\:ab\:-\:(a+b)+1\;\;…[2]\)
[2]に[1]を代入すると,4が書かれた円盤の枚数は,
\(\;\;\;\; 195\:-\:(a+b)+1\:=\:196\:-\:(a+b)\;\;…[3]\)
となる。そのため,4が書かれた円盤の枚数が最大になるのは,\(a+b\:\)が最小になるときである。
ここで,条件より,\(a,\:b\:は,2≦\:a\:<\:b\:\) … [4] となる自然数であり,\(a,\:b\:\)の間には,[1]の関係が成り立つ。
\(195\)を素因数分解すると,\(195\:=\:3\times 5\times 13\: \)であり,\(a,\:b\: \)がとりえる値は,条件 [4] を考慮すると,次の3通りである。
\(\;\;\;\;(a,\:b)\:=\: \{ (3,\:65),\:(5,\:39),\:(13,\:15) \} \)
各値の組の合計\((a+b)\)は,それぞれ,68, 44, 28であるので,\((a+b)\)が最小になる組み合わせは,
\(\;\;a\:=\:13,\:b\:=\:15\:\)のときである。… ①,② の答。
このときの,円盤の枚数は,\((a-1)(b-1)\:=\:12\times 14\:=\:168\)(枚) … ③ の答
(注) 円盤の枚数は,[3] に,\(a+b=28\)を代入して,\(196 – 28 = 168\)(枚) で OK.
\(\;\; \begin{eqnarray} (m-1)\times 2 &=& 2a (cm), \\ (n-1)\times 2 &=& 2b (cm) \end{eqnarray} \)
である。
4隅の円盤の中心を結んでできる長方形の面積が \(780 cm^2\) だから,次の式が成り立つ。
\(\;\;\;\; 2a\times 2b\:=\:780\;→\:ab\:=\:195\;\;…[1]\)
4が書かれた円盤は,\(縦\:m\:-\:2\:=\:a\:-\:1\;\)枚,\(横\:n\:-\:2\:=\:b\:-\:1\;\)枚の長方形になるので,全部で,\((a\:-\:1)(b\:-\:1)\)枚である。
\(\;\;\;\; (a\:-\:1)(b\:-\:1)\:=\:ab\:-\:(a+b)+1\;\;…[2]\)
[2]に[1]を代入すると,4が書かれた円盤の枚数は,
\(\;\;\;\; 195\:-\:(a+b)+1\:=\:196\:-\:(a+b)\;\;…[3]\)
となる。そのため,4が書かれた円盤の枚数が最大になるのは,\(a+b\:\)が最小になるときである。
ここで,条件より,\(a,\:b\:は,2≦\:a\:<\:b\:\) … [4] となる自然数であり,\(a,\:b\:\)の間には,[1]の関係が成り立つ。
\(195\)を素因数分解すると,\(195\:=\:3\times 5\times 13\: \)であり,\(a,\:b\: \)がとりえる値は,条件 [4] を考慮すると,次の3通りである。
\(\;\;\;\;(a,\:b)\:=\: \{ (3,\:65),\:(5,\:39),\:(13,\:15) \} \)
各値の組の合計\((a+b)\)は,それぞれ,68, 44, 28であるので,\((a+b)\)が最小になる組み合わせは,
\(\;\;a\:=\:13,\:b\:=\:15\:\)のときである。… ①,② の答。
このときの,円盤の枚数は,\((a-1)(b-1)\:=\:12\times 14\:=\:168\)(枚) … ③ の答
(注) 円盤の枚数は,[3] に,\(a+b=28\)を代入して,\(196 – 28 = 168\)(枚) で OK.

1, 2の問題は,とりあえず,絵を描いてみることですね。1, 2 の絵が描けたら円盤の数値がどのように配置されるかは,なんとなく,判ってくると思います。
4隅は,数値2が配置され,一番外側(周囲)の4隅以外は,数値3が配置される。そして,周囲以外(長方形/正方形)の内部には,すべて,数値4が配置される。
ここで,m, nは3以上の整数 という条件から,周囲には2と3が書かれた円盤が混在し,内部には4が書かれた円盤が少なくとも一つ配置されることがわかります。3の枚数は,上辺と下辺が m – 2 枚,左辺と右辺は n-2 枚になります。4の枚数は,(m-2)×(n-2)枚です。
3の問題は上記の規則を m と n の両方を x とおいて,x の2次式を作り,x を求めることになります。
4の問題は,いわゆる,整数問題というもので,問題で与えられた条件から,文字 a, b を使った2つの関係式を作ります。ひとつは,長方形の面積から算出されるもので,縦/横がそれぞれ a+1, b+1 枚の時,円の中心を結んでできる長方形の縦と横の長さは,2a と 2b に
になることが理解できれば,[1] の式が導かれます。
また,4が書かれた円盤の枚数は,1,2 の問題から,(m-2)×(n-2)枚とわかっていますので,これに,m=a+1, n=b+1 を代入して 文字 a, b を使って面積を表すと[2] の式が導かれます。
[1] 式で,a, b はいずれも整数であることから 195 の約数である必要があり,
条件[4] を考えない場合,a, b の取りえる値の範囲は,{ 1, 3, 5, 13, 15, 39, 65, 195 }であり,条件[4] を考慮すると,答に記載した通りの3組の数値に絞られます。あとは,この3組の数値の和が最小なものを選べば良いことになります。