2019 (H31) 熊本県 数学 B問題 大問6
\(\)



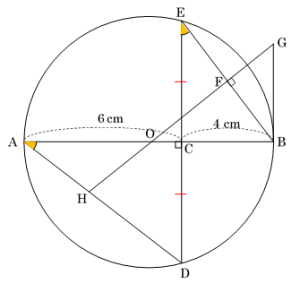
6 右の図は,点\(\:O\:\)を中心とする円で,線分\(\:AB\:\)は円の直径である。点\(\:C\:\)は線分\(\:OB\:\)上にあり,\(2\:\)点\(\:D,\:E\:\)は,\(C\:\)を通る線分\(OB\:\)の垂線と円\(\:O\:\)との交点である。点\(\:F\:\)は線分\(\:BE\:\)上にあって,\(OF \perp BE\:\)である。また,点\(\:G\:\)は\(\:OF\:\)の延長と\(\:B\:\)における円\(\:O\:\)の接線との交点であり,点\(\:H\:\)は\(\:FO\:\)の延長と線分\(\:AD\:\)との交点である。
このとき,次の各問いに答えなさい。ただし,根号がつくときは,根号のついたままで答えること。
(1) \(\triangle ADC\:\)∽\(\triangle BGF\:\)であることを証明しなさい。
\(BG\:\)は円\(\:O\:\)の接線なので,\(\angle GBC\:=\:90°\:\)であり,
\(\:BG/\!/DE\:\)であるので,平行線の錯角の関係より,\(\angle GBE\:=\:\angle BED\;\dots\;①\)
同一弧に対する円周角なので,\(\angle BED\:=\:\angle BAD\;\dots\;②\)
①,②より,\(\angle FBG\:=\:\angle CAD\;\dots\;③\)
仮定より,\(\angle BFG\:=\:\angle ACD (\:=\: 90°)\;\dots\;④\)
③,④より,\(\triangle ADCと\triangle BGF\:\)において,
2組の角が,それぞれ等しいので,\(\triangle ADC\:\)∽\(\triangle BGF\)

\(\:BG/\!/DE\:\)であるので,平行線の錯角の関係より,\(\angle GBE\:=\:\angle BED\;\dots\;①\)
同一弧に対する円周角なので,\(\angle BED\:=\:\angle BAD\;\dots\;②\)
①,②より,\(\angle FBG\:=\:\angle CAD\;\dots\;③\)
仮定より,\(\angle BFG\:=\:\angle ACD (\:=\: 90°)\;\dots\;④\)
③,④より,\(\triangle ADCと\triangle BGF\:\)において,
2組の角が,それぞれ等しいので,\(\triangle ADC\:\)∽\(\triangle BGF\)

(2) \(AB\:=\:10\:cm,\:BC\:=\:4\:cm\:\)のとき
① 線分\(\:CE\:\)の長さを求めなさい。
\(\triangle ADC\:と\:\triangle EBC\:\)において,
\(\angle DCA\:=\:\angle BCE\:(\:=\:90°\:)\)
\(\angle DAC\:=\:\angle BEC\:\)(同一の円周角)
であるので,\(\triangle ADC\:\)∽\(\triangle EBC\:\)
相似な図形の対応する辺の比は等しいので,
\(CA : CE\:=\:DC : BC \:⇒\: CE\times DC\:=\:CA\times BC\)
点\(\:E\:\)と点\(\:D\:\)は,半径\(\:AB\:\)を対称軸にした線対称の位置にあるので,対称軸からの距離は等しい。
\(CE\:=\:DC\) を上式に代入して,
\(CE^2 \:=\: CA \times BC \:=\: 6\times 4 \:=\: 24\)
\(CE\:>\:0\:\)より,\(CE\:=\:\sqrt{24}\:=\:2\sqrt{6} cm\)
\(\angle DCA\:=\:\angle BCE\:(\:=\:90°\:)\)
\(\angle DAC\:=\:\angle BEC\:\)(同一の円周角)
であるので,\(\triangle ADC\:\)∽\(\triangle EBC\:\)
相似な図形の対応する辺の比は等しいので,
\(CA : CE\:=\:DC : BC \:⇒\: CE\times DC\:=\:CA\times BC\)
点\(\:E\:\)と点\(\:D\:\)は,半径\(\:AB\:\)を対称軸にした線対称の位置にあるので,対称軸からの距離は等しい。
\(CE\:=\:DC\) を上式に代入して,
\(CE^2 \:=\: CA \times BC \:=\: 6\times 4 \:=\: 24\)
\(CE\:>\:0\:\)より,\(CE\:=\:\sqrt{24}\:=\:2\sqrt{6} cm\)
② 線分\(\:DH\:\)の長さを求めなさい。

\(\triangle ADC\:\)∽\(\triangle BGF\:\)より,\(\angle ADC\:=\:\angle BGF\;\dots\;①\)
\(\triangle ACD\:と\:\triangle OBG\:\)において,\(\angle ACD\:=\:\angle OBG\;\dots\;②\)
①,②より,\(\triangle ACD\)∽\(\triangle OBG\) で相似比は,\(AC : OB \:=\: 6 : 5\)
(2)より,\(CD\:=\:CE\:=\:2\sqrt{6}\)であるので,
\(BG\:=\:2\sqrt{6}\times \frac{5}{6}\:=\:\frac{5\sqrt{6}}{3} \:cm\)
また,\(\angle CAD \:=\: \angle BOG \:=\: \angle AOH \)で
\(\triangle HOA\:\)は,Hを頂点とする二等辺三角形である。
点\(\:H\:\)から半径\(\:OA\:\)に垂線を下し,交点\(\:I\:\)とすると,交点\(\:I\:\)は\(\:OA\:\)を2等分する。
\(\triangle OIH\:\)と\(\triangle OBG\:\)は相似であり,
相似比は,\(OI : OB \:=\: 2.5 : 5 \:=\: 1 : 2\)
したがって,\(HI \:=\: GB\times \frac{1}{2} \:=\: \frac{5\sqrt{6}}{6} \:cm\)
\(\begin{eqnarray} 三角形OADの面積 &=& OA(底辺)\times CD(高さ) ÷ 2 \\ &=& 5\times 2\sqrt{6} ÷ 2 \\ &=& 5\sqrt{6} \:cm^2 \end{eqnarray} \)
\(\begin{eqnarray} 三角形OAHの面積 &=& OA(底辺)\times HI(高さ) ÷ 2 \\ &=& 5\times \frac{5\sqrt{6}}{6} ÷ 2 \\ &=& \frac{25\sqrt{6}}{12} \:cm^2 \end{eqnarray} \)
\(\begin{eqnarray} 三角形ODHの面積 &=& \triangle OADの面積\:-\:\triangle OAHの面積 \\ &=& 5\sqrt{6}-\frac{25\sqrt{6}}{12} \\ &=& \frac{35\sqrt{6}}{12} \:cm^2 \end{eqnarray} \)
\(\triangle OAD\:\)と\(\triangle ODH\:\)の面積比は,2つの三角形の底辺を \(\:AD,\:DH\:\)とすると,高さが同じなので,\(AD : DH\:\) になる。
\(DH : AD\:=\:\frac{35\sqrt{6}}{12} : 5\sqrt{6} \:=\: \frac{7}{12} : 1 \:=\: 7 : 12\)
\(AD\:\)の長さは,三平方の定理より,
\(\sqrt{(2\sqrt{6})^2 + 6^2} \:=\:\sqrt{24 + 36} \:=\: 2\sqrt{15} \:cm\)
したがって,\(DH = AD\times \frac{7}{12} \:=\: \frac{7\sqrt{15}}{6} \:cm\)
\(\triangle ACD\:と\:\triangle OBG\:\)において,\(\angle ACD\:=\:\angle OBG\;\dots\;②\)
①,②より,\(\triangle ACD\)∽\(\triangle OBG\) で相似比は,\(AC : OB \:=\: 6 : 5\)
(2)より,\(CD\:=\:CE\:=\:2\sqrt{6}\)であるので,
\(BG\:=\:2\sqrt{6}\times \frac{5}{6}\:=\:\frac{5\sqrt{6}}{3} \:cm\)
また,\(\angle CAD \:=\: \angle BOG \:=\: \angle AOH \)で
\(\triangle HOA\:\)は,Hを頂点とする二等辺三角形である。
点\(\:H\:\)から半径\(\:OA\:\)に垂線を下し,交点\(\:I\:\)とすると,交点\(\:I\:\)は\(\:OA\:\)を2等分する。
\(\triangle OIH\:\)と\(\triangle OBG\:\)は相似であり,
相似比は,\(OI : OB \:=\: 2.5 : 5 \:=\: 1 : 2\)
したがって,\(HI \:=\: GB\times \frac{1}{2} \:=\: \frac{5\sqrt{6}}{6} \:cm\)
\(\begin{eqnarray} 三角形OADの面積 &=& OA(底辺)\times CD(高さ) ÷ 2 \\ &=& 5\times 2\sqrt{6} ÷ 2 \\ &=& 5\sqrt{6} \:cm^2 \end{eqnarray} \)
\(\begin{eqnarray} 三角形OAHの面積 &=& OA(底辺)\times HI(高さ) ÷ 2 \\ &=& 5\times \frac{5\sqrt{6}}{6} ÷ 2 \\ &=& \frac{25\sqrt{6}}{12} \:cm^2 \end{eqnarray} \)
\(\begin{eqnarray} 三角形ODHの面積 &=& \triangle OADの面積\:-\:\triangle OAHの面積 \\ &=& 5\sqrt{6}-\frac{25\sqrt{6}}{12} \\ &=& \frac{35\sqrt{6}}{12} \:cm^2 \end{eqnarray} \)
\(\triangle OAD\:\)と\(\triangle ODH\:\)の面積比は,2つの三角形の底辺を \(\:AD,\:DH\:\)とすると,高さが同じなので,\(AD : DH\:\) になる。
\(DH : AD\:=\:\frac{35\sqrt{6}}{12} : 5\sqrt{6} \:=\: \frac{7}{12} : 1 \:=\: 7 : 12\)
\(AD\:\)の長さは,三平方の定理より,
\(\sqrt{(2\sqrt{6})^2 + 6^2} \:=\:\sqrt{24 + 36} \:=\: 2\sqrt{15} \:cm\)
したがって,\(DH = AD\times \frac{7}{12} \:=\: \frac{7\sqrt{15}}{6} \:cm\)
全体的に説明がだらだらとなってしまいました。
# ちょっと判りにくくなっているかもしれません。
(2) ② については,いろいろな解き方があると思います。
もっと良い方法 等ありましたら,コメントをお願いします。